Torsional vibrations

Example from the PscFunctions package

With the help of routines of the PscFunctions package one can visualize torsional vibration of the cylindrical shaft.  
 At the beginning we create a parametric equation of the surface of the cylindrical   shaft together with the bases . For that we use the PR(x,a,w)  function of the package.

>    restart;
with(PscFunctions):
L:=6: r:=2: # Length and radius of the cylinder
x:=(u,v)->r*cos(u)*(PR(v,-r,r)-PR(v,L,r)):
y:=(u,v)->r*sin(u)*(PR(v,-r,r)-PR(v,L,r)):
z:=(u,v)->L*PR(v,0,L):
plot3d([x(u,v),y(u,v),z(u,v)],u=0..2*Pi,v=-r..L+r,scaling=CONSTRAINED,grid=[21,41],style=WIREFRAME,color=BLACK,style=HIDDEN,labels=["X","Y","Z"],axes=BOXED);
'X'=x(u,v);
'Y'=y(u,v);
'Z'=z(u,v);

[Maple Plot]

X = 2*cos(u)*(1/4*abs(v+2)-1/4*abs(v)-1/4*abs(v-6)+1/4*abs(v-8))
Y = 2*sin(u)*(1/4*abs(v+2)-1/4*abs(v)-1/4*abs(v-6)+1/4*abs(v-8))
Z = 3+1/2*abs(v)-1/2*abs(v-6)

Then we create solution of the initial boundary value problem .  
Consider a circular shaft built in at the lower end and twisted by a couple applied to the upper end. At initial time the upper end is released. In the shaft torsional vibration will start. It is known that the twist angle satisfies to the wave equation. Let the initial twist angle varies linearly along the shaft. As the lower base is fastened the boundary value of the twist angle is equal to 0, i.e. theta(0,t) = 0 . 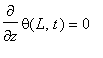As the upper base is free the second boundary condition at the upper basis becomes diff(theta(L,t),z) = 0 . To construct solution we shall execute even continuation of function theta(z,0)  concerning the point x=L , then execute odd continuation concerning the point x=0 , and then extend resulting function periodically from segment [ -2L, 2L ]  to entire axis. For realization of such continuation we use FPeriodic  routine of the PscFunctions  package. The routine generates a function that represents periodic extension of the function segment to entire real axis. Then from obtained periodic function F(x)  we shall create solution of the wave equation by formula d'Alembert. We suppose that the initial velocity is equal to 0.

>    f:=tau->2*tau/L:   # initial twist angle
f1:=FPeriodic(f,-infinity..L,style='even'):
F:=FPeriodic(f1,0..2*L,style='odd'):
plot(F('x'),'x'=-12..36,thickness=2);
U:=(x,t)->(F(x-t)+F(x+t))/2:
print(`The Twist Angle of the Shaft`);
print('U(x,t)'=U('x','t'));

[Maple Plot]

`The Twist Angle of the Shaft`

U(x,t) = 1/2*signum(-12+Mod(x-t+12,24))*(2-1/3*abs(-6+abs(-12+Mod(x-t+12,24))))+1/2*signum(-12+Mod(x+t+12,24))*(2-1/3*abs(-6+abs(-12+Mod(x+t+12,24))))
U(x,t) = 1/2*signum(-12+Mod(x-t+12,24))*(2-1/3*abs(-6+abs(-12+Mod(x-t+12,24))))+1/2*signum(-12+Mod(x+t+12,24))*(2-1/3*abs(-6+abs(-12+Mod(x+t+12,24))))

Naw we can create a parametric equation of the   twisted   shaft surface .
In the parametric equation of cylinder the parameter u  appears as angle. Therefore at generation the equation of the twisted cylinder this parameter should be incremented by the magnitude of the twist angle, i.e.

X(u,v)=x(u+U(z(u,v),t),v),  Y(u,v)=y(u+U(z(u,v),t),v),  Z(u,v)=z(u+U(z(u,v),t),v) ,

where U(z,t)= theta(z,t)   is obtained solution of the wave equation (a magnitude of twist angle in section z  at moment t ). This makes possible to construct the shape of the shaft surface at any point of time. Let's show this vibration.

>    X:=(u,v,t)->x(u+U(z(u,v),t),v):
Y:=(u,v,t)->y(u+U(z(u,v),t),v):
Z:=(u,v,t)->z(u+U(z(u,v),t),v):
plots[animate](plot3d,[[X(u,v,t),Y(u,v,t),Z(u,v,t)],u=0..2*Pi,v=-r..L+r,grid=[21,41],style=HIDDEN,color=BLACK,labels=["X","Y","Z"],axes=BOXED],t=0..4*L-1,frames=20,scaling=CONSTRAINED,orientation=[40,60]);

[Maple Plot]