Plate with a Circular Hole

Example from the PscFunctions package

The PscFunctions package is an excellent tool for making visual illustrations of solutions in many fields of applied mathematics and mechanics .
We shall consider examples of visualization of the stress in the infinite flat plate with a circular hole.
Here is equation of the infinite plate with a circular hole.

>    xp:=(r,v)->(1+QR(r,1))*cos(v):
yp:=(r,v)->(1+QR(r,1))*sin(v):
plot3d([xp(u,v),yp(u,v),0],u=0..5,v=0..2*Pi,view=[-3..3,-3..3,-1..1],axes=BOXED,grid=[26,31],scaling=CONSTRAINED,orientation=[-90,0],labels=["X","Y","Z"]);
'x'=xp(u,v);
'y'=yp(u,v);

[Maple Plot]

x = (1/2+1/2*u+1/2*abs(u-1))*cos(v)
y = (1/2+1/2*u+1/2*abs(u-1))*sin(v)

Let the plate is expose to the homogeneous tension of the magnitude P  in X direction. Then the stresses sigma[r] , sigma[theta] , tau[r,theta]   in the plate with a circular hole are computed by formulas:

>    r:='r': v:='v': P:='P': a:='a':
Sr:=(r,v)->P/2*(1-a^2/r^2)+P/2*(1+3*a^4/r^4-4*a^2/r^2)*cos(2*v):
St:=(r,v)->P/2*(1+a^2/r^2)-P/2*(1+3*a^4/r^4)*cos(2*v):
Trt:=(r,v)->-P/2*(1-3*a^4/r^4+2*a^2/r^2)*sin(2*v):
'Sr'=Sr(r,v);
'St'=St(r,v);
'Trt'=Trt(r,v);
P:=1:   # magnitude of tension   
a:=1:   # radius of the hole

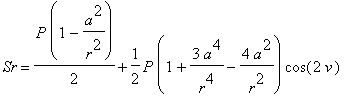
Sr = 1/2*P*(1-a^2/r^2)+1/2*P*(1+3*a^4/r^4-4*a^2/r^2)*cos(2*v)
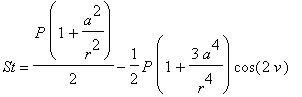
St = 1/2*P*(1+a^2/r^2)-1/2*P*(1+3*a^4/r^4)*cos(2*v)
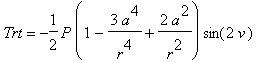
Trt = -1/2*P*(1-3*a^4/r^4+2*a^2/r^2)*sin(2*v)

Let us use these functions as color option to draw a region of the plate with a hole.

>    plot3d([xp(r,v),yp(r,v),0],'r'=1..6,v=0..2*Pi,view=[-4..4,-4..4,-1..1],axes=BOXED,grid=[26,31],scaling=CONSTRAINED,orientation=[-90,0],labels=["X","Y","Z"],color=Sr(a+QR(r,a),v),style=patchnogrid,title=`Sr stress`);

[Maple Plot]

To understand this color picture we shall draw a color box of the function sigma[r] = Sr(r,v) . Next figure will represent a graphical palette of the stress.

>    plot3d([x,0,z],x=-1..1,z=0..P,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","Sr"],orientation=[-90,90],tickmarks=[0,0,5]);

[Maple Plot]

Here is pattern of the sigma[theta]  stress.

>    plot3d([xp(u,v),yp(u,v),0],u=1..5,v=0..2*Pi,view=[-3..3,-3..3,-1..1],axes=BOXED,grid=[26,31],scaling=CONSTRAINED,orientation=[-90,0],labels=["X","Y","Z"],color=St(a+QR(u,a),v),style=patchnogrid,title=`St stress`);

[Maple Plot]

Next figure will represent a graphical palette of the sigma[theta]  stress.

>    plot3d([x,0,z],x=-1..1,z=-P..3*P,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","St"],orientation=[-90,90],tickmarks=[0,0,4]);

[Maple Plot]

Here is pattern of the sigma[x]  stress.

>    r:='r':
Sx:=(r,v)->Sr(r,v)*cos(v)^2+St(r,v)*sin(v)^2-Trt(r,v)*sin(2*v):
plot3d([xp(r,v),yp(r,v),0],r=1..5,v=0..2*Pi,view=[-3..3,-3..3,-1..1],axes=BOXED,grid=[26,31],scaling=CONSTRAINED,orientation=[-90,0],labels=["X","Y","Z"],color=Sx(a+QR(r,a),v),style=patchnogrid,title=`Sx stress`);

[Maple Plot]

Next figure will represent a graphical palette of this stress.

>    plot3d([x,0,z],x=-1..1,z=0..3*P,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","Sx"],orientation=[-90,90],tickmarks=[0,0,6]);

[Maple Plot]