![[Maple Plot]](DemoImages/Splines1.gif)
Splines
Example from the PscFunctions package
With the help of routines of the PscFunctions package one can obtain general parametric equations of splines.
The
CPscSpline
routine generates a sequence of two or three functions that represents parametric equation of the spline with specified end conditions.
The spline curve passes through the given point set (first argument of the procedure). The type of end conditions is determined by the second (optional) argument.
| > | restart; with(PscFunctions): x,y:=CPscSpline([[0,0],[-12,4],[-9,6],[-15,14],[-6,12],[-15/2,18],[-3,16],[0,22],[3,16],[15/2,18],[6,12],[15,14],[9,6],[12,4],[0,0]],endpoints=natural): plot([x(t),y(t),t=0..14],thickness=2,scaling=CONSTRAINED,color=BLACK); X=x(t); Y=y(t); |
![[Maple Plot]](DemoImages/Splines1.gif)
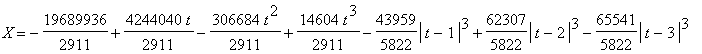
![]()
![]()
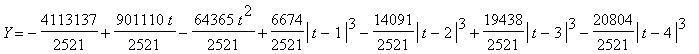
![]()
![]()
The
fPscSpline
routine computes an
expression that represents
explicit equation of the
polynomial spline
of any degre.
In the following example equations of some splines of different degree passing through the same points constructed.
| > | LL:=[[-5,-2],[-3,-3],[1,2],[3,2],[4,0],[5,-1],[6,0],[8,-2],[9,4],[12,-1],[15,4],[20,3],[24,-1],[25,0]]: Z2:=x->fPscSpline(LL,x,degree=2): Z3:=x->fPscSpline(LL,x,degree=3): Z4:=x->fPscSpline(LL,x,degree=4): Z5:=x->fPscSpline(LL,x,degree=5): pnts:=plots[pointplot](LL,symbolsize=20): pys:=plot([Z2(x),Z3(x),Z4(x),Z5(x)],x=LL[1,1]..LL[nops(LL),1],thickness=2,scaling=CONSTRAINED,color=[BLACK,BLUE,GREEN,RED]): plots[display](pnts,pys); 'Z3'=Z3(x); |
![[Maple Plot]](DemoImages/Splines8.gif)
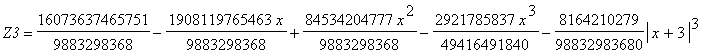
![]()
![]()
![]()