Deflection of a simple beam, which carries concentrated loads .
Example from the PscFunctions package
With the help of procedures of the package one can visualize surface stress of the loaded beam
.
In some cases it is possible to get an unified formular equation of a bending moment and deflection of a beam, which carries piecewise loadings
.
Consider a beam freely supported at the endpoints. Let the beam has length L=8 and carries 3 concentrated loads. Let it has rectangular cross section and its width is equal to
b
and the height is equal to
h
. The procedure
FPolyline
of the package generates the explicit equation of a piecewise linear function
M(x)
.
| > | restart; with(PscFunctions): LX:=[3/2,4,13/2]: # X - coordinates of load points LP:=[1,-1,1]: # Value of point loads L:=8: # Length of a beam R1:=sum(LP[i]*(1-LX[i]/L),i=1..nops(LP)): # reaction at supports LM:=[seq((R1-sum(LP[i],i=1..k-1))*LX[k]+sum(LP[i]*LX[i],i=1..k-1),k=1..nops(LP))]: # values of bending moments at the load points LL:=[[0,0],seq([LX[i],LM[i]],i=1..nops(LP)),[L,0]]: M:=FPolyline(LL): print(`Bending Moment: M`=M(x)); plot(M(x),x=0..L,thickness=2); |
![]()
![[Maple Plot]](DemoImages/SimpleBeam2.gif)
Deflection can be found from formula
y(x)
=
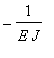
![int(int(M(x),x),x)+C[1]*x+C[2]](DemoImages/SimpleBeam4.gif) , where
, where
![]() and
and
![]() are some constants, which should be determined from the boundary conditions
y(0)=0
and
y(L)=0
. Then we create LY list, which consist of pairs of numbers [
are some constants, which should be determined from the boundary conditions
y(0)=0
and
y(L)=0
. Then we create LY list, which consist of pairs of numbers [
![]() ] (coordinate of a load point and a magnitude of deflection at this point). Deflection function
y(x)
will be a piecewise-cubic polynomial passing through these points, i.e. a cubic spline. Its unified formular expression can be obtained with the help of routine
FPscSpline
(LY,endpoints='natural')
of the package.
] (coordinate of a load point and a magnitude of deflection at this point). Deflection function
y(x)
will be a piecewise-cubic polynomial passing through these points, i.e. a cubic spline. Its unified formular expression can be obtained with the help of routine
FPscSpline
(LY,endpoints='natural')
of the package.
| > | E:=2: h:=2: b:=1: J:=b*h^3/12: i1:=int(M(x),x)/(E*J): i2:=int(i1,x): yy:=t->eval(subs(x=t,i2)): C1:=-yy(L)/L: # C2=0 y0:=x->yy(x)+C1*x: Y:=[seq(y0(LX[i]),i=1..nops(LX))]: LY:=[[0,0],seq([LX[i],Y[i]],i=1..nops(LP)),[L,0]]: Z:=FPscSpline(LY,endpoints='natural'): print(`Deflection: y(x)`=Z(x)); py:=plot(Z(x),x=0..L,thickness=2,scaling=CONSTRAINED,color=BLACK): Lar:=seq(plottools[arrow]([LX[i],Z(LX[i])+LP[i]],[LX[i],Z(LX[i])],.01, .1, .1, color=BLACK),i=1..nops(LP)): plots[display](Lar,py); |
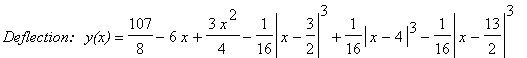
![[Maple Plot]](DemoImages/SimpleBeam9.gif)
Then we construct the equation of a surface of a beam. At the beginning we generate a parametric equation
x(u,v), y(u,v), z(u,v)
of a surface of the undeformed beam. For this purpose we use
SCuboid
routine of the
PSCFunctions
package. In view of hypothesis of the flat cross sections then we create the equation
Xb(u,v), Yb(u,v), Zb(u,v)
of the surface of the deformed beam. Longitudinal stress of the beam is computed by formula
![sigma[x] = -M(x)*z/J](DemoImages/SimpleBeam10.gif) , where
M(x)
is a bending moment at the cross section with coordinate
x.
To color a surface of the beam in various colors depending on magnitudes of the longitudinal stress we create the
ColorBeam
function, which computes this stress. This function is used as the option
color
of the
plot3d
procedures.
, where
M(x)
is a bending moment at the cross section with coordinate
x.
To color a surface of the beam in various colors depending on magnitudes of the longitudinal stress we create the
ColorBeam
function, which computes this stress. This function is used as the option
color
of the
plot3d
procedures.
| > | SC:=SCuboid(L,b,h): x:=(u,v)->SC[1](u,v): y:=(u,v)->SC[2](u,v)-b/2: z:=(u,v)->SC[3](u,v)-h/2: Uder:=diff(Z('x'),'x'): U1:=unapply(Uder,'x'): Xb:=(u,v)->x(u,v)-U1(x(u,v))/sqrt(1+U1(x(u,v))^2)*z(u,v): Yb:=(u,v)->y(u,v): Zb:=(u,v)->Z(x(u,v))+1/sqrt(1+U1(x(u,v))^2)*z(u,v): ColorBeam:=(u,v)->-M(x(u,v))*z(u,v)/J: plot3d([Xb(u,v),Yb(u,v),Zb(u,v)],u=0..2*L+2*h,v=-h..h+b,scaling=CONSTRAINED,grid=[61,21],axes=BOXED,labels=["X","Y","Z"],color=-ColorBeam(u,v),orientation=[60,60]); |
![[Maple Plot]](DemoImages/SimpleBeam11.gif)
Here is the equation of the surface of the undeformed beam.
| > | 'X'=x(u,v); 'Y'=y(u,v); 'Z'=z(u,v); |
![]()
![]()
![]()
![]()
To understand the color picture of the deformed beam we shall draw a color box of the function
![]() .
.
| > | Zmin:=-9/8: Zmax:=9/8: x:='x': z:='z': plot3d([x,0,z],x=-1..1,z=Zmin..Zmax,axes=BOXED,grid=[21,21],color=-z,style=patchnogrid,labels=["","","Sx"],orientation=[-90,90]); |
![[Maple Plot]](DemoImages/SimpleBeam17.gif)