RunningSpline.html

Running Spline

Example from the PscFunctions package

Using PscFunctions routines it is possible to obtain a line of new exact formula solutions of initial boundary value problems for the wave equation .
Let the initial velocity of the string is equal to 0 and the string is fixed at both ends. That the solution of the one-dimensional wave equation was twice continuously differentiable it is necessary that the function of initial displacement u(x,0)=f (x) was twice differentiable, has vanished at the ends of the string, and the fitting conditions f"(0) =0 , f"(L) =0 satisfied. Such function, for example, may be a B-spline basis function of 3-rd degree. We can create its explicit equation using the FPscHermite routine

`>`	restart; with(PscFunctions): Lxy := [[-1,0],[0,0],[1,1],[2,4],[3,1],[4,0],[5,0]]: fe:=FPscHermite(Lxy,x,derivatives=[smooth],endpoints=natural): B3:=(t,a)->subs(x=t-a,fe): B3(x,1); plot(B3(x,1),x=0..8,thickness=3,color=BLACK);

Let's take the B3(x,1) function as initial displacement of the string. For periodic extension of initial function from segment onto entire axis we use the function stc(x,w) . It is an elementary function and can be represented as 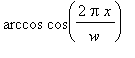. Let us substitute oddly and periodically extended function in d'Alembert formula. We suppose the initial velocity is equal to 0. Using the obtained solution u(x,t) we shall draw graphs of the string at the start times.

`>`	L:=8: # length a:=1: # wave velocity Z:=x->B3(x,1): # initial displacementof u:=(x,t)->((-1)^floor((x+at)/L)Z(stc(x+at,2L))+\ (-1)^floor((x-at)/L)Z(stc(x-at,2L)))/2: plot([u(x,0),u(x,0.25),u(x,0.5),u(x,0.75),u(x,1),u(x,1.25),u(x,1.5)],x=0..L,thickness=1,color=BLACK,linestyle=[1,2,3,4,5,6]);

Here are graphs of the string at later points of time.

`>`	plot([u(x,2.25),u(x,2.5),u(x,2.75),u(x,2.9),u(x,3.1),u(x,3.25)],x=0..L,thickness=1,color=[BLUE,CYAN,MAGENTA,NAVY,aquamarine,CORAL]);

Here is graph of the string on the move.

`>`	plots[animate]( plot, [u(x,t),x=0..L,thickness=2,color=BLACK], t=0..16, frames=33 );

Let's mark, that we construct the exact solution u(x,t) of the wave equation. It is twice continuously differentiable and it is satisfied to fitting conditions. Besides it fulfils all boundary and initial conditions. The constructed solution looks like the following:

`>`	'u'=u(x,t);
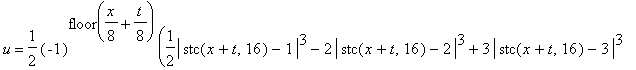
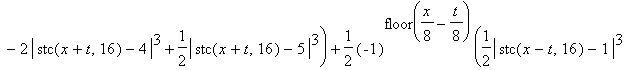