Equations of polylines

Example from the PscFunctions package

With the help of routines of the PscFunctions package users can create equations of continuous polygonal lines.
The FPolyline   routine generates  equation of the continuous polygonal lines passing through the given points.

>    restart;
with(PscFunctions):
f1:=FPolyline([[0,-1],[1,1],[2,0],[3,2],[4,1]]):
plot(f1(x),x=-1..6,thickness=2,scaling=CONSTRAINED,color=BLACK);
print('y'=f1(x));

[Maple Plot]

y = abs(x)-3/2*abs(x-1)+3/2*abs(x-2)-3/2*abs(x-3)+1/2*abs(x-4)

The FPscPolyline  routine generates  explicit equation of the piecewise smooth continuous function. This function on various segments of the real axis originally is given by the various expressions .

>    f1:=x->sin(Pi*x): f2:=x->x-1: f3:=x->2*(4-x): f4:=x->(x-4)*(x-6):
p9:=FPscPolyline([f1,f2,f3,f4],[0,1,3,4,6]):
plot(p9(x),x=-1..7,thickness=2,scaling=CONSTRAINED,color=BLACK);
print('y'=p9(x));

[Maple Plot]

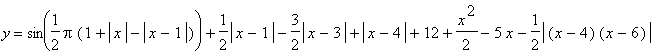
y = sin(1/2*Pi*(1+abs(x)-abs(x-1)))+1/2*abs(x-1)-3/2*abs(x-3)+abs(x-4)+12+1/2*x^2-5*x-1/2*abs((x-4)*(x-6))

The CPscPolyline  routine generates a sequence of two or three functions of one variable that represents a parametric equation of a piecewise smooth continuous curve.
Here is an example of construction of the parametric equation of the closed curvilinear polyline. Its contour is bounded from below by the piece of a sinusoid, on the right by the rectilinear segment, from above by the circular arc, and from the left by segment of parabola.

>    fx1:=t->t: fy1:=t->3/10*sin(Pi*t):
fx2:=t->1: fy2:=t->t:
fx3:=t->(1+cos(Pi*t))/2: fy3:=t->1+sin(Pi*t)/2:
fx4:=t->t*(1-t): fy4:=t->1-t:
crv5:=CPscPolyline([[fx1,fy1],[fx2,fy2],[fx3,fy3],[fx4,fy4]],[[0,1],[0,1],[0,1],[0,1]]):
plot([crv5(t),t=0..4],-0.2..1.2,0..1.5,thickness=2,scaling=CONSTRAINED,color=BLACK);
print('x'=crv5[1](t));
print('y'=crv5[2](t));

[Maple Plot]

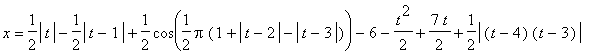
x = 1/2*abs(t)-1/2*abs(t-1)+1/2*cos(1/2*Pi*(1+abs(t-2)-abs(t-3)))-6-1/2*t^2+7/2*t+1/2*abs((t-4)*(t-3))
y = 3/10*sin(1/2*Pi*(1+abs(t)-abs(t-1)))+1/2*abs(t-1)-1/2*abs(t-2)+1/2*sin(1/2*Pi*(1+abs(t-2)-abs(t-3)))-1/2*abs(t-3)+1/2*abs(t-4)

With the help of the CPscPolyline routine it is possible to create parametric equations of the majority of piecewise smooth continuous curves. It will be possible if the parametric equations of the pieces of the curve are known.