Longitudinal wave

Example from the PscFunctions package

With the help of routines of the package one can visualize   longitudinal waves .  
 Let us explore a longitudinal wave of a rectangular rod.
Let the rod with the square cross section is fastened at the left end and its right end is free. The stretching force is applied to the right end and in the start time it is released. The rod starts to be compressed and then to be extended. As a result along the rod longitudinal waves will propagate. Let's show this process.
At the beginning we shall generate the equation of the surface of the strainless rod. We can make it with the help of   SCuboid  routine of the package.

>    restart;
with(PscFunctions):
L:=4:  # Length of a rod
h:=1:  # Height of a rod
x,y,z:=SCuboid(L,h,h):  
plot3d([x(u,v),y(u,v),z(u,v)],u=0..2*L+2*h,v=-h..2*h,scaling=CONSTRAINED,grid=[6*(2*L+2*h)+1,6*3*h+1],axes=BOXED,style=HIDDEN,color=BLACK,orientation=[-120,60],labels=[X,Y,Z]);

[Maple Plot]

Generate the function U(x,t)  representing longitudinal displacement of the rod points  This function satisfies to the homogeneous wave equation. To construct solution we shall execute even continuation of the function of initial displacement f(x)  concerning point x=L ,  then execute odd continuation concerning point x=0  and then we shall extend resulting function periodically from segment [-2*L, 2*L]  to entire axis. The obtained periodical function we shall substitute in the formula of d'Alembert. 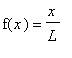Let's take initial displacement in the linear form f(x) = x/L  and execute the indicated above extension using FPeriodic  routine of the package.

>    f:=x->x/L:
f1:=FPeriodic(f,-infinity..L,style='even'):
F:=FPeriodic(f1,0..2*L,style='odd'):
print('F(x)'=F(x));
plot(F('x'),'x'=-2*L..4*L,thickness=2);

F(x) = signum(-8+Mod(x+8,16))*(1-1/4*abs(-4+abs(-8+Mod(x+8,16))))

[Maple Plot]

Function Mod(x,a)  used in the previous formulas gives the remainder on division of the first argument by the second.
Now with the help of obtained periodic function F(x)  we shall construct solution of the wave equation (suppose that the initial velocity is equal to 0).

>    U:=(x,t)->(F(x-t)+F(x+t))/2:
plots[animate]( plot, [U(x,t),x=0..L,thickness=2], t=0..4*L-1/2, frames=8*L);

[Maple Plot]

Then we can construct the equation of the surface of the rod at any moment. It will look like the following X(u,v)=x(u,v)+U(x(u,v),t), Y(u,v)=y(u,v), Z(u,v)=z(u,v) , where U(x,t)  is the obtained solution of the wave equation. Generate these oscillations.

>    X:=(u,v,t)->x(u,v)+U(x(u,v),t):
Y:=(u,v,t)->y(u,v):
Z:=(u,v,t)->z(u,v):
plots[animate](plot3d,[[X(u,v,t),Y(u,v,t),Z(u,v,t)],u=0..2*L+2*h,v=-h..2*h,grid=[6*(2*L+2*h)+1,6*3*h+1],style=HIDDEN,color=BLACK,labels=["X","Y","Z"],axes=BOXED],t=0..4*L-1,frames=4*L,scaling=CONSTRAINED);

[Maple Plot]