![X[x] = -2*P/Pi](DemoImages/ConcentratedLoad1.gif)
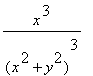 ,
,
![Y[x] = -2*P/Pi](DemoImages/ConcentratedLoad3.gif)
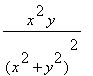 ,
,
![Y[y] = -2*P/Pi](DemoImages/ConcentratedLoad5.gif)
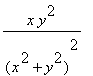 .
.
Effect of concentrated loads at an elastic half plane
Example from the PscFunctions package
With the help of routines of the PscFunctions package it is possible to make visual illustrations of solutions in many fields of applied mathematics and mechanics
.
Consider a flat elastic medium on the one hand restricted by horizontal line. In some point of boundary the concentrated force
P
is applied transversely. It is required to find stress in the medium. The solution of this problem is known. Stress is computed by the following formulas
![X[x] = -2*P/Pi](DemoImages/ConcentratedLoad1.gif)
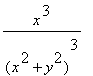 ,
,
![Y[x] = -2*P/Pi](DemoImages/ConcentratedLoad3.gif)
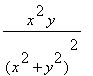 ,
,
![Y[y] = -2*P/Pi](DemoImages/ConcentratedLoad5.gif)
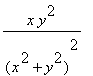 .
.
The stress becomes infinite at the load point. To depict them as a color palette the functions
![]() ,
,
![]() ,
,
![]() it is necessary to restrict somehow at the load point. This can be made by using the
PscMin
,
PscMax
or
PscMinMax
functions of the package.
it is necessary to restrict somehow at the load point. This can be made by using the
PscMin
,
PscMax
or
PscMinMax
functions of the package.
Consider an example. Let us point
x
-axis vertically downwards and
y
-axis point horizontally to the right. Let us generate the equation of the half plane. If to use function
![]() as the option
color=
as the option
color=
![]() the large negative value of the stress at the load point will disfigure a picture. But using the function
TensXx=
PscMax
(
the large negative value of the stress at the load point will disfigure a picture. But using the function
TensXx=
PscMax
(
![]() ,
,
![]() ) it is possible to improve a graphical representation. The function
TensXx(x,y)
coincides with function
) it is possible to improve a graphical representation. The function
TensXx(x,y)
coincides with function
![]() in all points in which its value is more than
minXx
and is equal to this value in the others.
in all points in which its value is more than
minXx
and is equal to this value in the others.
| > | xx:=(u,v)->QR(u,0): # x coordinate function of a half-plane yy:=(u,v)->v: # y coordinate function of a half-plane PP:=1: # applied force Xx:=(x,y)->-2*PP/Pi*x^3/(x^2+y^2)^2: # Xx stress minXx:=-1.6: # conditionally taken limitation of stress from below TensXx:=(u,v)->PscMax(Xx(xx(u,v),yy(u,v)),minXx): plot3d([xx(u,v),yy(u,v),0],u=-0.5..2,v=-1.5..1.5,axes=BOXED,grid=[51,61],labels=["X","Y","Z"],orientation=[0,0],view=[-0.5..2,-1.5..1.5,-1..1],scaling=CONSTRAINED,color=TensXx(u,v),style=PATCHNOGRID,title=`Xx stress`); |
![[Maple Plot]](DemoImages/ConcentratedLoad15.gif)
To understand this color picture we shall draw a color box of the function Xx(x,y) . Next figure will represent the graphical palette of this stress.
| > | plot3d([x,0,z],x=-1..1,z=minXx..0,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","Xx"],orientation=[-90,90],tickmarks=[0,0,5]); |
![[Maple Plot]](DemoImages/ConcentratedLoad16.gif)
It is interesting to look at the stress
![]() . It is known that it is computed by formula
. It is known that it is computed by formula
 = -2*P*x/(Pi*(x^2+y^2))](DemoImages/ConcentratedLoad18.gif) . To representation of this function it is convenient to trim its value from below using
PscMax
routine of the package.
. To representation of this function it is convenient to trim its value from below using
PscMax
routine of the package.
| > | Rr:=(x,y)->-2*PP/Pi*x/(x^2+y^2): minRr:=-2: TensRr:=(u,v)->PscMax(Rr(xx(u,v),yy(u,v)),minRr): plot3d([xx(u,v),yy(u,v),0],u=-0.5..2,v=-1.5..1.5,axes=BOXED,grid=[51,61],labels=["X","Y","Z"],orientation=[0,0],view=[-0.5..2,-1.5..1.5,-1..1],scaling=CONSTRAINED,color=TensRr(u,v),style=PATCHNOGRID,title=`Rr stress`); |
![[Maple Plot]](DemoImages/ConcentratedLoad19.gif)
Let us draw a color box of the function Rr, which will represent the graphical palette of this stress.
| > | plot3d([x,0,z],x=-1..1,z=minRr..0,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","Rr"],orientation=[-90,90],tickmarks=[0,0,6]); |
![[Maple Plot]](DemoImages/ConcentratedLoad20.gif)
In the previous example we have draw a stress in the half-plane which is subjected to one concentrated load. But we can analogously consider examples of several concentrated loads. Here is an example of effect of three concentrated loads.
| > | minXx:=-2.5: # conditionally taken limitation of Xx stress TensXx3:=(u,v)->PscMax(Xx(xx(u,v),yy(u,v)),minXx)+\ PscMax(Xx(xx(u,v),yy(u,v)-0.5),minXx)+\ PscMax(Xx(xx(u,v),yy(u,v)+0.5),minXx): plot3d([xx(u,v),yy(u,v),0],u=-0.1..1,v=-1..1,axes=BOXED,grid=[51,61],labels=["X","Y","Z"],orientation=[0,0],view=[-0.1..1,-1..1,-0.1..0.1],scaling=CONSTRAINED,color=TensXx3(u,v),style=PATCHNOGRID,title=`Xx stress`); |
![[Maple Plot]](DemoImages/ConcentratedLoad21.gif)
Next figure represents a graphic palette of the Xx stress.
| > | z:='z': plot3d([x,0,z],x=-0.5..0.5,z=minXx..0,axes=BOXED,grid=[21,21],color=z,style=patchnogrid,labels=["","","Xx"],orientation=[-90,90],tickmarks=[0,0,5],scaling=CONSTRAINED); |
![[Maple Plot]](DemoImages/ConcentratedLoad22.gif)