Billiards.html

Rectangular billiards

Example from the PscFunctions package

With the help of routines of the PscFunctions package it is possible to transform equations of curves and surfaces .
Here the problem of creation equation of the path of a point inside a flat rectangular box is solved. Friction misses and the law of reflection is observed.
Let the curve is given by the parametric equation x=x(t), y=y(t) . The equation of the curve obtained by multiple interior reflection from the boundaries of the rectangular region xl<x<xr, yd<y<yu looks like the following:

, (1)
, (2)

where stc(x,w) is a sawtooth function from the PscFunctions package.
Here is an example of the polygonal line obtained by multiple interior reflection of a straight line from boundaries of the rectangle. The ray starts at the point (3/4,1/2) and has the initial direction along the vector (2,1).

> restart;
with(PscFunctions):
xl:=-1: xr:=1: yd:=-2: yu:=2: # reflection boundary
x:=t->3/4+t*2:
y:=t->1/2+t:
xrefl:=t->xl+stc(x(t)-xl,2*(xr-xl)):
yrefl:=t->yd+stc(y(t)-yd,2*(yu-yd)):
crv:=plot([xrefl(t),yrefl(t),t=0..7.8],thickness=2,\
scaling=CONSTRAINED,color=BLACK,numpoints=500):
rec:=plottools[rectangle]([xl,yu], [xr,yd],linestyle=2):
plots[display](crv,rec, scaling=constrained);

The path of a point in rectangular billiards represents a polygonal line obtained at multiple reflections of a rectilinear ray from the boundaries of the rectangle. The formulas presented above are applicable for modelling of such path.
Let from the point ( ) the infinitesimal ball in the direction of the vector ( ) darts out. Friction misses. If boundaries are not present the ball would move on the line with the equation , , where t is time (parameter along a ray), c is a velocity, is a slope angle of the ray to the x-axis. The equation of the polygonal line obtained after multiple interior reflections from the boundaries will look like (1), (2). The following example shows as the point goes inside the rectangle

> xl:=-1: xr:=1: yd:=-2: yu:=2: # reflection boundary
x0:=-1/2: y0:=1/2: # starting point
alpha:=arctan(5/7): # angle of a starting direction
x:=t->x0+t*cos(alpha):
y:=t->y0+t*sin(alpha):
xrefl:=t->xl+stc(x(t)-xl,2*(xr-xl)):
yrefl:=t->yd+stc(y(t)-yd,2*(yu-yd)):
rec := plots[display](plottools[rectangle](\
[xl,yu],[xr,yd],linestyle=2)):
plots[animate](plot,[[xrefl(t),yrefl(t),t=0..T],color=BLACK,numpoints=500],T=1..68,scaling=CONSTRAINED,thickness=2,frames=35,background=rec );

In the following example if a slope ratio of the path at the starting point is rational, i.e. 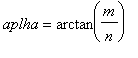and m,n are integers, then the path will be closed. Otherwise it never will come back in the starting point and gradually will paint over all area of the rectangle.

> xl:=-1: xr:=1: yd:=-1: yu:=1: # reflection boundary
x0:=0: y0:=0: # starting point
alpha:=arctan(sqrt(2)): # angle of a starting direction
x:=t->x0+t*cos(alpha):
y:=t->y0+t*sin(alpha):
xrefl:=t->xl+stc(x(t)-xl,2*(xr-xl)):
yrefl:=t->yd+stc(y(t)-yd,2*(yu-yd)):
plot([xrefl(t),yrefl(t),t=0..300],color=BLACK,numpoints=5000,thickness=1);

Here is the parametric equation of this path.

`>`	'X'=xrefl(t); 'Y'=yrefl(t);