Bend of a Channel

Example from the PscFunctions package

With the help of procedures of the package one can visualize a stress on the surface of the loaded beam . In some cases it is possible to obtain the unified formular equation of the bending moment and deflection of the beam .
Let the beam has length L=30 and carries 3 concentrated loads.  The procedure FPolyline of the package generates the explicit equation of a piecewise linear function. In this example the function will represent a bending moment M(x) .

>    restart;
with(PscFunctions):
LX:=[7,15,23]:     # X - coordinates of load points
LP:=[4,-5,4]:      # Value of point loads
L:=30:             # Length of a beam
R1:=sum(LP[i]*(1-LX[i]/L),i=1..nops(LP)): # reaction at support
LM:=[seq((R1-sum(LP[i],i=1..k-1))*LX[k]+sum(LP[i]*LX[i],i=1..k-1),k=1..nops(LP))]:
LL:=[[0,0],seq([LX[i],LM[i]],i=1..nops(LP)),[L,0]]:
M:=FPolyline(LL):
print(`Bending Moment:  M`=M(x));
plot(M(x),x=0..L,thickness=2);

`Bending Moment:  M` = 3/4*abs(x)-2*abs(x-7)+5/2*abs(x-15)-2*abs(x-23)+3/4*abs(x-30)

[Maple Plot]

Equation of the bent  curve can be obtained as follows

>    E:=2: h:=6: b:=3: J:=54:
i1:=int(M(x),x)/(E*J):
i2:=int(i1,x):
yy:=t->eval(subs(x=t,i2)):
C1:=-yy(L)/L:
y0:=x->yy(x)+C1*x:
Y:=[seq(y0(LX[i]),i=1..nops(LX))]:
LY:=[[0,0],seq([LX[i],Y[i]],i=1..nops(LP)),[L,0]]:
U:=FPscSpline(LY,endpoints='natural'):
print(`Deflection:   y(x)`=U(x));
py:=plot(U(x),x=0..L,thickness=2,scaling=CONSTRAINED,color=BLACK):
Lar:=seq(plottools[arrow]([LX[i],U(LX[i])+LP[i]],[LX[i],U(LX[i])],.1, .5, .1, color=BLACK),i=1..nops(LP)):
plots[display](Lar,py);

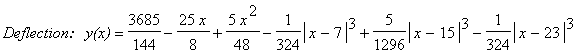
`Deflection:   y(x)` = 3685/144-25/8*x+5/48*x^2-1/324*abs(x-7)^3+5/1296*abs(x-15)^3-1/324*abs(x-23)^3

[Maple Plot]

Now we shall construct equation of the surface of the undeformed channel .

>    fd1:=CPolyline([[0,0],[1,0],[1,1],[5,1],[5,0],[6,0]],[0,1,2,6,7,8]):
fu1:=CPolyline([[0,3],[1,3],[1,2],[5,2],[5,3],[6,3]],[0,1,2,6,7,8]):
xx:=t->fd1[1](t):
f1:=t->fd1[2](t):
f2:=t->fu1[2](t):
Sect:=DRectDomain(xx,f1,f2):
Sc1:=(u,v)->Sect[1](u,v):
Sc2:=(u,v)->Sect[2](u,v):
H:=30:
p1:=FPolyline([[-H,H],[0,0],[8,0],[H+8,H]]):
p2:=FPolyline([[-H,H],[0,0],[3,0],[H+3,H]]):
P2:=(u,v)->H*PR(p1(u)+p2(v),0,H):
fd3:=CPolyline([[0,-3],[1,-3],[1,-1],[5,-1],[5,-3],[6,-3]],[0,1,2,6,7,8]):fu3:=CPolyline([[0,0],[1,0],[1,0],[5,0],[5,0],[6,0]],[0,1,2,6,7,8]):
Cover:=DPscRing([fd3],[fu3],param2=6+H..3+H):
xr:=(u,v)->P2(u,v):
yr:=(u,v)->Sc2(u,v)+Cover[2](u,v):
zr:=(u,v)->Sc1(u,v)-3:
plot3d([xr(u,v),yr(u,v),zr(u,v)],u=-H..8+H,v=-H..6+H,axes=BOXED,scaling=CONSTRAINED,orientation=[40,65],grid=[(2*H+8)*1+1,(2*H+6)*1+1]);

[Maple Plot]

In view of hypothesis of the flat cross sections we create the equation Xb(u,v), Yb(u,v), Zb(u,v)  of the surface of the deformed channel. Longitudinal stresses of the beam are computed by formula sigma[x] = -M(x)*z/J , where M(x)  is a bending moment at the cross section with coordinate x .  To color the surface of the beam in various colors depending on magnitudes of the longitudinal stress we create ColorBeam  function. It computes this stress. We use this function as the option color  of the plot3d  procedures.  

>    Uder:=diff(U(x),x):
U1:=unapply(Uder,x):
Xb:=(u,v)->xr(u,v)-U1(xr(u,v))/sqrt(1+U1(xr(u,v))^2)*zr(u,v):
Yb:=(u,v)->yr(u,v):
Zb:=(u,v)->U(xr(u,v))+1/sqrt(1+U1(xr(u,v))^2)*zr(u,v):
ColorBeam:=(u,v)->-M(xr(u,v))*zr(u,v)/J:
plot3d([Xb(u,v),Yb(u,v),Zb(u,v)],u=-H..8+H,v=-H..6+H,axes=BOXED,scaling=CONSTRAINED,orientation=[40,65],grid=[(2*H+8)*1+1,(2*H+6)*1+1],color=-ColorBeam(u,v),tickmarks=[0,0,0]);

[Maple Plot]

To understand this color picture we shall draw a color box of the function sigma[x] .

>    Smax:=(21/2)*3/J: Smin:=-Smax:
plot3d([x,0,z],x=-1..1,z=Smin..Smax,axes=BOXED,grid=[21,21],color=-z,style=patchnogrid,labels=["","","Sx"],orientation=[-90,90]);

[Maple Plot]